A smooth cylinder lying on a __________ is in neutral equilibrium.
Curved surface
Convex surface
Horizontal surface
None of these
Correct Answer :
C. Horizontal surface
Related Questions
The velocity ratio for the first system of pulleys is (where n is the number of pulleys.)
n
n²
2n
2n - 1
The force induced in the string BC due to the load W as shown in the below figure is 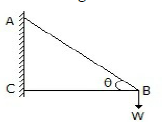
W sinθ
W cosθ
W tanθ
W cotθ
The angular velocity (in rad/s) of a body rotating at N revolutions per minute is
πN/60
πN/180
2πN/60
2πN/180
If a number of forces are acting at a point, their resultant will be inclined at an angle θ with the horizontal, such that
tanθ = ΣH/ΣV
tanθ = ΣV/ΣH
tanθ = ΣV × ΣH
tanθ = √(ΣV + ΣH)
Moment of inertia of a hollow circular section, as shown in the below figure about an axis perpendicular to the section, is __________ than that about X-X axis. 
Two times
Same
Half
None of these
A ladder is resting on a rough ground and leaning against a smooth vertical wall. The force of friction will act
Downward at its upper end
Upward at its upper end
Zero at its upper end
Perpendicular to the wall at its upper end
Least force required to draw a body up the inclined plane is W sin (plane inclination + friction angle) applied in the direction
Along the plane
Horizontally
Vertically
At an angle equal to the angle of friction to the inclined plane
The energy possessed by a body, for doing work by virtue of its position, is called
Potential energy
Kinetic energy
Electrical energy
Chemical energy
According to principle of moments
If a system of coplanar forces is in equilibrium, then their algebraic sum is zero
If a system of coplanar forces is in equilibrium, then the algebraic sum of their moments about any point in their plane is zero
The algebraic sum of the moments of any two forces about any point is equal to moment of the resultant about the same point
Positive and negative couples can be balanced
The bellow figure shows the two equal forces at right angles acting at a point. The value of force R acting along their bisector and in opposite direction is 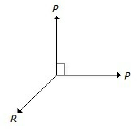
P/2
2P
√2 × P
P/√2
A force is completely defined when we specify
Magnitude
Direction
Point of application
All of the above
The velocity of a particle moving with simple harmonic motion is __________ at the mean position.
Zero
Minimum
Maximum
None of these
Lami's theorem states that
Three forces acting at a point will be in equilibrium
Three forces acting at a point can be represented by a triangle, each side being proportional to force
If three forces acting upon a particle are represented in magnitude and direction by the sides of a triangle, taken in order, they will be in equilibrium
If three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two
Forces are called coplanar when all of them acting on body lie in
One point
One plane
Different planes
Perpendicular planes
If the gravitational acceleration at any place is doubled, then the weight of a body will be
g/2
g
√2.g
2g
A single force and a couple acting in the same plane upon a rigid body
Balance each other
Cannot balance each other
Produce moment of a couple
Are equivalent
The total motion possessed by a body, is called
Impulsive force
Mass
Weight
Momentum
Which of the following is not a scalar quantity?
Mass
Volume
Density
Acceleration
Which of the following do not have identical dimensions?
Momentum and impulse
Torque and energy
Torque and work
Moment of a force and angular momentum.
Efficiency of a screw jack is given by (where α = Helix angle, and φ = Angle of friction.)
tan(α + φ)/tanα
tanα/tan (α + φ)
tan(α - φ)/tanα
None of these
In the lever of third order, load W, effort P and fulcrum F are oriented as follows
W between P and F
F between W and P
P between W and F
W, P and F all on one side
Two balls of equal mass and of perfectly elastic material are lying on the floor. One of the balls with velocity v is made to strike the second ball. Both the balls after impact will move with a velocity
v
v/2
v/4
v/8
A weight of 1000 N can be lifted by an effort of 80 N. If the velocity ratio is 20, the machine is
Reversible
Non-reversible
Ideal
None of these
The moment of a force
Is the turning effect produced by a force, on the body, on which it acts
Is equal to the product of force acting on the body and the perpendicular distance of a point and the line of action of the force
Is equal to twice the area of the triangle, whose base is the line representing the force and whose vertex is the point, about which the moment is taken
All of the above
The slope on the road surface generally provided on the curves is known as
Angle of friction
Angle of repose
Angle of banking
None of these
The coefficient of friction depends upon
Nature of surfaces
Area of contact
Shape of the surfaces
All of the above
A force while acting on a body may
Change its motion
Balance the forces, already acting on it
Give rise to the internal stresses in it
All of these
The horizontal range of a projectile (R) is given by
R = u² cos2α/g
R = u² sin2α/g
R = u² cosα/g
R = u² sinα/g
D' Alembert's principle is used for
Reducing the problem of kinetics to equivalent statics problem
Determining stresses in the truss
Stability of floating bodies
Designing safe structures
Two like parallel forces are acting at a distance of 24 mm apart and their resultant is 20 N. It the line of action of the resultant is 6 mm from any given force, the two forces are
15 N and 5 N
20 N and 5 N
15 N and 15 N
None of these
