The resultant of the following three couples 20 kg force, 0.5 m arm, +ve sense 30 kg force, 1 m arm, -ve sense 40 kg force, 0.25 m arm, +ve sense having arm of 0.5 m will be
20 kg, -ve sense
20 kg, + ve sense
10 kg, + ve sense
10 kg, -ve sense
Correct Answer :
A. 20 kg, -ve sense
Related Questions
The M.I. of hollow circular section about a central axis perpendicular to section as compared to its M.I. about horizontal axis is
Same
Double
Half
Four times
The slope on the road surface generally provided on the curves is known as
Angle of friction
Angle of repose
Angle of banking
None of these
A machine having an efficiency less than 50%, is known as
Reversible machine
Non-reversible machine
Neither reversible nor non-reversible machine
Ideal machine
A flywheel on a motor goes from rest to 1000 rpm in 6 sec. The number of revolutions made is nearly equal to
25
50
100
250
The unit of angular acceleration is
N-m
m/s
m/s2
rad/s2
A trolley wire weighs 1.2 kg per meter length. The ends of the wire are attached to two poles 20 meters apart. If the horizontal tension is 1500 kg find the dip in the middle of the span
2.5 cm
3.0 cm
4.0 cm
5.0 cm
The necessary condition for forces to be in equilibrium is that these should be
Coplanar
Meet at one point
Both (A) and (B) above
All be equal
The unit of power in S.I. units is
Horsepower
Joule
Watt
kg-m
Which of the following are vector quantities?
Linear displacement
Linear velocity
Linear acceleration
All of these
Two non-collinear parallel equal forces acting in opposite direction
Balance each other
Constitute a moment
Constitute a couple
Constitute a moment of couple
Centre of gravity of a thin hollow cone lies on the axis at a height of
One-fourth of the total height above base
One-third of the total height above base
One-half of the total height above base
Three-eighth of the total height above the base
The moment of inertia of a rectangular section 3 cm wide and 4 cm deep about X-X axis is
9 cm4
12 cm4
16 cm4
20 cm4
In a framed structure, as shown in the below figure, the force in the member BC is 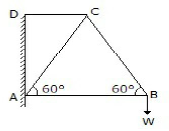
W/√3 (compression)
W/√3 (tension)
2W/√3 (compression)
2W/√3 (tension)
Three forces acting on a rigid body are represented in magnitude, direction and line of action by the three sides of a triangle taken in order. The forces are equivalent to a couple whose moment is equal to
Area of the triangle
Twice the area of the triangle
Half the area of the triangle
None of these
In a single threaded worm and worm wheel, the number of teeth on the worm is 50. The diameter of the effort wheel is 100 mm and that of load drum is 50 mm. The velocity ratio is
50
100
200
400
Which of the following is a vector quantity?
Energy
Mass
Momentum
Angle
The centre of gravity a T-section 100 mm × 150 mm × 50 mm from its bottom is
50 mm
75 mm
87.5 mm
125 mm
The range of projectile on a downward inclined plane is ________ the range on upward inclined plane for the same velocity of projection and angle of projection.
Less than
More than
Equal to
None of These
When trying to turn a key into a lock, following is applied
Coplanar force
Non-coplanar forces
Moment
Couple
If a number of forces are acting at a point, their resultant is given by
(ΣV)2 + (ΣH)2
√[(ΣV)2 + (ΣH)2]
(ΣV)2 +(ΣH)2 +2(ΣV)(ΣH)
√[(ΣV)2 +(ΣH)2 +2(ΣV)(ΣH)]
Which one of the following statements is not correct?
The tangent of the angle of friction is equal to coefficient of friction
The angle of repose is equal to angle of friction
The tangent of the angle of repose is equal to coefficient of friction
The sine of the angle of repose is equal to coefficient to friction
Moment of inertia of a rectangular section having width (b) and depth (d) about an axis passing through its C.G. and parallel to the depth (d), is
db3/12
bd³/12
db³/36
bd³/36
If two bodies having masses m1 and m2 (m1>m2) have equal kinetic energies, the momentum of body having mass m1 is _________ the momentum of body having mass m2.
Equal to
Less than
Greater than
None of these
The velocity of a body on reaching the ground from a height h, is
2.√(gh)
√(gh)
√(2gh)
2g.√h
Coplanar non-concurrent forces are those forces which __________ at one point, but their lines of action lie on the same plane.
Meet
Do not meet
Either A or B
None of these
According to law of triangle of forces
Three forces acting at a point will be in equilibrium
Three forces acting at a point can be represented by a triangle, each side being proportional to force
If three forces acting upon a particle are represented in magnitude and direction by the sides of a triangle, taken in order, they will be in equilibrium
If three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two
Two bodies of masses m1 and m2 are hung from the ends of a rope, passing over a frictionless pulley as shown in the figure below. The acceleration of the string will be 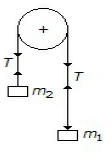
g (m1 - m2)/(m1 + m2)
2g (m1 - m2)/(m1 + m2)
g (m1 + m2)/(m1 - m2)
2g (m1 + m2)/(m1 - m2)
Which of the following is a scalar quantity?
Force
Speed
Velocity
Acceleration
If a body is acted upon by a number of coplanar non-concurrent forces, it may
Rotate about itself without moving
Move in any one direction rotating about itself
Be completely at rest
All of these
The resolved part of the resultant of two forces inclined at an angle θ in a given direction is equal to
The algebraic sum of the resolved parts of the forces in the given direction
The sum of the resolved parts of the forces in the given direction
The difference of the forces multiplied by the cosine of θ
The sum of the forces multiplied by the sine of θ
